|
[ Chapter start ] [ Previous page ] [ Next page ] 13.12 Problems* = Difficult, ** = Very difficult, *** = Extremely difficult 13.1 (Errors, 30 min.) Change a <= b to a >= b in line 4 in module reference in Section 13.2.1 . Simulate the testbench (write models for the five logic cell models not shown in Section 13.2.1 ). How many errors are there, and why? Answer: 56. 13.2 (False paths, 15 min.) The following code forces an output pin to a constant value. Perform a timing analysis on this model and comment on the results. module check_critical_path_2 (a, z); input a; output z; supply1 VDD; supply0 VSS; nd02d0 b1_i3 (.a1(a), .a2(VSS), .zn(z)); // 2-input NAND 13.3 (Timing loops, 30 min.) The following code models a set–reset latch with feedback to implement a memory element. Perform a timing analysis on this model and comment on the results. module check_critical_path_3 (s, r, q, qn); input s, r; output q, qn; supply1 VDD; supply0 VSS; nr02d0 b1_i1 (.a1(s), .a2(qn), .zn(q)); // 2-input NOR nr02d0 b1_i2 (.a1(r), .a2(q), .zn(qn)); // 2-input NOR 13.4 (Simulation script, 30 min.) Perform a gate-level simulation of the comparator/MUX in Section 13.2.3 . Write a script to set input values and so on. 13.5 (Verilog loops, 30 min.) Change the index from integer to reg (width three) in each loop in testbench.v from Section 13.2 . Explain the simulation result. 13.6 (Verilog time, 30 min.) Remove '#1' from line 15 in testbench.v from Section 13.2 . Explain carefully the simulation result. 13.7 ( Infinite loops, 30 min.) Construct an HDL program that loops infinitely on a UNIX machine (with no output file!) and explain how the following helps: 28920 p1 R 0:30 verilog infinite_loop.v 13.8 (Verilog graphics, 30 min.) Experiment with graphical waveform dumps from Verilog. For example, in VeriWell you need to include the following statement:
The file Dump file
veriwell.dmp
should appear. Next, select
File...
, then 13.9 (Unknowns, 30 min.) Explain, using truth tables, the function of primitive G6 in module mx21d1 from Section 13.2.1 . Hint: Consider unknown propagation. Eliminate primitive G6 as follows and use simulation to compare the two models: not G3(N3,s); and G4(N4,i0,N3), G5(N5,s,i1); or G7(z,N4,N5); 13.10 (Data books, 10 min.) Explain carefully what you safely can and cannot deduce from the data book figures in Table 13.16 .
13.11 (Synthesis, 30 min.) Synthesize comp_mux_rrr.v in Section 13.7 . What type and how many sequential elements result? Answer: 16. 13.12 (Place and route, 60 min.) Route both comp_mux.v ( Section 13.2 ) and comp_mux_rrr.v ( Section 13.7 ) using an FPGA. What fraction of the chip is used? Answer: For an Actel 1415 FPGA, comp_mux_rrr.v uses about 10 percent of the available logic. 13.13 (Timing analysis, 60 min.) Perform timing analysis on a routed version of comp_mux.v from Section 13.2 . Use worst-case commercial conditions. 13.14 (***NAND gate delay, 120 min.) The following example of a six-input NAND gate illustrates the difference between transistor-level and other levels of simulation. A designer once needed a delay element (do not ask why!). Looking at the data book they found a six-input NAND gate had the right delay, but they did not know what to do with the other five inputs. So they tied all six inputs together. This is a horrendous error, but why? Hint: You might have to simulate a structural model using both digital simulation and a circuit-level simulation in order to explain. 13.15 ( Logic systems, 30 min.) Compare the 12 value system of Table 13.5 with the IEEE 1164 standard and explain: Which logic values are equivalent in both systems, which logic values have no equivalents, and why there is a difference in the number of values (12 versus 9) when both systems have the same number of logic levels and logic strengths? 13.16 (VHDL overloaded functions, 30 min.) Write a definition for the type stdlogic_table used in the and function in Section 13.3.2 , constant and_table:stdlogic_table Compile, simulate, and test the and function. 13.17 (**Scheduling transactions in VHDL, 60 min.) (From an example in the VHDL LRM.) Consider this assignment to an integer S in a VHDL process: S <= reject 15 ns inertial 12 after 20 ns, 18 after 41 ns; Assume that at the time this signal assignment is executed, the driver for S in the process has the following contents (the first entry is the current driving value): now +3ns +12ns +13ns +20ns +42ns This is called the projected output waveform (times are relative to the current time). The LRM states the rule for updating a projected output waveform consists of the deletion of zero or more previously computed transactions (called old transactions) from the projected output waveform, and the addition of the new transactions, as follows:
If the initial delay is inertial delay, the projected output waveform is further modified as follows:
For the purposes of marking transactions, any two successive null transactions in a projected output waveform are considered to have the same value component. Using these rules compute the new projected output waveform. 13.18 (*** awk , 120 min.) Write an awk program with the following specification to compare two simulations: # program to check two files with the format: # to check agreement within time tolerance delta (by default 0.1) # Use: check file1 file2 [delta] 13.19 (VITAL, 60 min.) Simulate the model, sdf_testbench , shown in Section 13.5.5 , with and without back-annotation timing information in SDF_b.sdf . 13.20 (Formal verification, 60 min.) Write a cheat sheet explaining how to run your formal verification tool. Repeat the example in Section 13.8.1 . 13.21 (***Beetle problem) (Based on a problem by Seitz.) A planet has many geological gem mazes: A maze covers a square km or so, on a 10 mm grid; a maze cell is 10 mm by 10 mm and gems lie at cell centers; there is a path from every maze cell to every other; on average one in 64 cells has an overhead opening; on average one in seven cells has a single gem; there are no gems under overhead openings. You are to design a gem-mining beetle ASIC with the following inputs: a nominal 1 MHz single-phase clock, CLK ; wall sensors: WL , WR , WF , WB (wall to left/right/forward/behind); light sensors: LL , LR , LF , LB ( light left/right/forward/behind); low-battery indicator: BLOW ; gem sensor: GEM (directly over a gem); opening sensor: OPEN (when under an opening). All signals are active high and the light sensor outputs are mutually exclusive. The beetle ASIC must produce the following (mutually exclusive) signals: move forward, MF ; move backward, MB ; turn 90 degrees clockwise, TC ; turn 90 degrees anticlockwise, TA ; pick up a gem, PICKUP ; throw gem up and out of overhead opening, THROWUP ; jump up to surface and shut down, SHUTUP . The beetle specifications and limitations are as follows: Beetles are dropped into the maze to find the gems; beetles must find gems and carry them to an opening; beetles can eject gems through openings; beetles can carry only one gem at a time. A beetle move is one of the following: taking one step (moving to an adjacent cell), turning 90 degrees, picking up a gem, ejecting a gem, jumping out of opening—all take the same time and energy. A battery can provide energy for about 200 moves before the low-battery signal comes on. After the low-battery warning is signaled the battery has energy for 50 moves to find an overhead opening, and the beetle must then eject itself for recharging. The cost of the beetle determines that we would like the probability of losing a beetle be below 0.01. The following describes a state machine to drive a beetle. Jim Rowson used a state-machine language that he developed—along with the first CAD tool that could automatically create state machines: inputs WL WL WR WB GEM LF LL LR LB OPEN BLOW; outputs MF=0 MB=0 TC=0 TA=0 PICKUP=0 THROWUP=0 SHUTUP=0; let getout = (BLOW|haveAgem) & (LL|LF|LR|LB); state resetState --> searchState haveAgem=0 SHUTUP=0; haveAgem & OPEN --> ejectstate, getout & LB --> turnAroundState, !haveAgem & GEM --> getGemState, state goFwdState --> MF searchState; state turnLState --> TA goFwdState; state turnRState --> TC goFwdState; state turnAroundState --> TC turnAgainState; state ejectState --> THROWUP !haveAgem searchState; state jumpState --> SHUTUP shutdownState; state getGemState --> PICKUP haveAgem searchState; state shutDownState --> SHUTUP shutDownState; state turnAgainState --> TC searchState;
13.22 (Switch-level simulation, 120 min.) Perform the switch-level simulation shown in Section 13.9 . 13.23 (**Simulation, 60 min.) (From a question posed by Ray Ryan to the VITAL timing group.) Suppose we have a two-input NAND gate (inputs I1 and I2, and output Q) with separate path delays from I1 to Q and from I2 to Q with delays as follows: ( tr01 => 10 ns, -- falling I1 -> rising Q tr10 => 7 ns ) -- rising I1 -> falling Q ( tr01 => 5 ns, -- falling I2 -> rising Q tr10 => 3 ns ) -- rising I1 -> falling Q 12 ns, 13 ns, 16 ns, 17 ns or other? 12 ns, 13 ns, 16 ns, 17 ns or other? 13 ns, 15 ns, 17 ns, 20 ns or other? 14 ns, 15 ns, 19 ns, 20 ns or other? 14 ns, 15 ns, 19 ns, 20 ns or other? 13 ns, 15 ns, 17 ns, 20 ns or other? In each case explain your answer using actual simulation results to help you. 13.24 (VHDL trace, 30 min.) Write a simple testbench and trace through the following VHDL behavioral simulation. use IEEE.std_logic_1164. all ; use IEEE.NUMERIC_STD. all ; port (A, B : in STD_LOGIC_VECTOR (2 downto 0); Y : out STD_LOGIC_VECTOR (2 downto 0)); architecture Behave of comp_mux is Y <= A after TPD when (A <= B) else B after TPD; 13.25 (VHDL simulator, 30 min.) Explain the steps in using your VHDL simulator. Are there separate compile, analyze, elaborate, initialization, and simulate phases. Where and when do they occur. How do you know? 13.26 (Debugging VHDL, 60 min.) Correct the errors in the following code: rset, updn, clock : in bit; carry : out bit; count : buffer integer range 0 to 255 ); architecture behave of counter8 is wait until clock'event and clock = '1'; if (rset = '1') then count <= 0; carry <= '0'; when '1' => count <= count + 1; if (count = 255) then carry <= '1'; else carry <= '0'; end if; when '0' => count <= count - 1; if (count = 0) then carry <= 1; else carry <= 0; end if; 13.27 (***VITAL flip-flop) The following VITAL code models a D flip-flop: LIBRARY ieee; USE ieee.Std_Logic_1164.all; USE ieee.Vital_Timing.all; USE ieee.Vital_Primitives.all; TimingChecksOn : BOOLEAN := TRUE; XGenerationOn : BOOLEAN := TRUE; tipd_Clock : DelayType01 := (0 ns, 0 ns); tipd_Data : DelayType01 := (0 ns, 0 ns); tsetup_Data_Clock : DelayType01 := (0 ns, 0 ns); thold_Data_Clock : DelayType01 := (0 ns, 0 ns); tpd_Clock_Q : DelayType01 := (0 ns, 0 ns); tpd_Clock_Qbar : DelayType01 := (0 ns, 0 ns)); PORT (Clock, Data: Std_Logic; Q,Qbar:OUT Std_Logic); ATTRIBUTE Vital_Level1 of gate : ARCHITECTURE IS TRUE; SIGNAL Clock_ipd : Std_Logic := 'X'; SIGNAL Data_ipd : Std_Logic := 'X'; Wire_Delay:BLOCK BEGIN -- INPUT PATH DELAYs (Clock_ipd, Clock, VitalExtendToFillDelay(tipd_Clock)); (Data_ipd, Data, VitalExtendToFillDelay(tipd_Data)); VitalBehavior : PROCESS (Clock_ipd, Data_ipd) CONSTANT Dff_tab:VitalStateTableType:= ( ( 'X', '-', '-', '-', 'X', 'X' ), -- Timing Violation ( '-', '\', '0', '-', '0', '1' ), -- Active Clock Edge ( '-', '\', '1', '-', '1', '0' ), ( '-', '\', 'X', '-', 'X', 'X' ), ( '-', '-', '0', '0', '0', '1' ), -- X Reduction ( '-', '-', '1', '1', '1', '0' ), ( '-', 'D', '-', '-', 'X', 'X' ), -- X Generation ( '-', 'B', '-', '-', 'S', 'S' ), -- Non-Active Clock Edge ( '-', 'X', '-', '-', 'S', 'S' )); -- Anything else generates X on Q and QBAR VARIABLE Tviol_Data_Clock : X01 := '0'; VARIABLE Tmkr_Data_Clock : TimeMarkerType; VARIABLE PrevData:Std_Logic_Vector(1 to 3):=(OTHERS=>'X'); VARIABLE Results:Std_Logic_Vector(1 to 2):=(OTHERS =>'X'); ALIAS Q_zd:Std_Logic IS Results(1); ALIAS Qbar_zd:Std_Logic IS Results(2); -- Output Glitch Detection Variables VARIABLE Q_GlitchData : GlitchDataType; VARIABLE Qbar_GlitchData : GlitchDataType; Data_ipd, "Data", Clock_ipd, "Clock", t_setup_hi => tsetup_Data_Clock(tr01), t_setup_lo => tsetup_Data_Clock(tr10), t_hold_hi => thold_Data_Clock(tr01), t_hold_lo => thold_Data_Clock(tr10), RefTransition => (Clock_ipd = '0'), HeaderMsg => InstancePath & "/DFF", TimeMarker => Tmkr_Data_Clock, Violation => Tviol_Data_Clock); Violation := Tviol_Data_Clock ; VitalStateTable(StateTable => Dff_tab, DataIn => (Violation, Clock_ipd, Data_ipd), VitalPropagatePathDelay (Q, "Q", Q_zd, Paths => (0 => (Clock_ipd'LAST_EVENT, VitalExtendToFillDelay(tpd_Clock_Q), TRUE), VitalExtendToFillDelay(tpd_Clock_Q), TRUE)), VitalPropagatePathDelay ( Qbar, "Qbar", Qbar_zd, Paths => (0 => (Clock_ipd'LAST_EVENT, VitalExtendToFillDelay(tpd_Clock_Qbar), TRUE), VitalExtendToFillDelay(tpd_Clock_Qbar), TRUE)), GlitchData => Qbar_GlitchData,
13.28 (VCD, 30 min.) Verilog can create a value change dump ( VCD ) file: module waves; reg clock; integer count; initial begin clock = 0; count = 0; ; #340 ; end always begin @ ( negedge clock); if (count == 7) count = 0; A VCD file contains header information, variable definitions, and the value changes for variables [Verilog LRM 15]. Try and explain the format of the file that results. 13.29 (*Formal verification, 60 min.) (Based on an example by Browne, Clarke, Dill, and Mishra.) A designer needs to fold an 8-bit ripple-carry adder into a small space on an ASIC and check the circuit extracted from the layout. With two 8-bit inputs, A and B , and a 1-bit carry Cin , exhaustively testing all possible inputs requires 2 17 or over 128,000 input vectors. Instead the designer selects a subset of tests. The three tests in Table 13.17 check that all the bits of the output can be '0' or '1' . The two tests in Table 13.18 make sure that the carry propagates through the adder, and that the adder can handle the largest numbers. The designer then repeats all of these five tests with the carry-in Cin set to '1' instead of '0' . Next the designer performs a series of 24 tests using the three patterns shown in Table 13.19 , with all eight possible combinations of '0' and '1' for x , y , and z . These patterns test each full adder in isolation for all possible sum inputs ( A and B ) and carry input ( Cin ). These tests appear comprehensive and reduce the number of vectors required from over 128,000 to 34. Confident, the designer releases the chip for fabrication. Unfortunately, the chip does not work. Which connections between adders did the designer’s tests fail to check?
13.30 (*BSIM1 parameters, 120 min.) SPICE models are tangled webs. For example, there are two formats for the 69 UCB BSIM1 transistor parameters: (1) using parameter names ( Table 13.15 ); and (2) without parameter names ( Table 13.20 ). MOSIS uses format (2). The first 58 parameters starting with VFB (19 rows of 3 parameters plus one, XPART ) are the same order in format (1) and (2). Format (2) uses two dummy parameters (zero) following XPART . The final nine parameters ( N0 to WND ) are the same order in both formats. There are 10 additional parameters that follow the n - and p -channel transistor parameters that model the n - and p -diffusion, respectively (in the same order in both formats). To complicate things further: (i) HSPICE, SPICE, and PSpice use different names for some parameters (for example PSpice uses VFB , HSPICE uses VFB0 ); (ii) HSPICE accepts names for the dummy parameters ( DUM1 and DUM2 ), but PSpice does not; (iii) HSPICE accepts the final parameter DS (though it is ignored), but PSpice does not ( DS models mask bias and can be neglected without too much fear). Convert the models shown in Table 13.20 to format (2) for your chosen simulator (PSpice LEVEL = 4 , HSPICE LEVEL = 13 ). Compare the resulting I DS – V DS characteristics with the LEVEL = 3 parameters ( Table 13.14 ) and the (PSpice) LEVEL = 4 parameters ( Table 13.15 ) for the G5 process. MOSIS has stored the results of its process runs in the format shown in Table 13.20 . 13.31 (**Nonreciprocal capacitance, 120 min.) (where d Q i / d V j are elements of matrix M ), show and thus that the rows of M sum to zero by showing that and three other similar equations for C DD , C SS , and C BB . and derive similar equations for the transient currents i S , i D , and i B . and, by deriving similar expressions for C DD , C SS , and C BB , show that the columns of M sum to zero. [ Chapter start ] [ Previous page ] [ Next page ] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

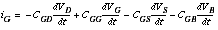 (13.10)
(13.10)



