15.4  Estimating ASIC Size

Table 15.3 shows some useful numbers for estimating ASIC die size. Suppose we wish to estimate the die size of a 40 k-gate ASIC in a 0.35 m m gate array, three-level metal process with 166 I/O pads. For this ASIC the minimum feature size is 0.35 m m. Thus l (one-half the minimum feature size) = 0.35 m m/2 = 0.175 m m. Using our data and Table 15.3 , we can derive the following information. We know that 0.35 m m standard-cell density is roughly 5 ¥ 10 ^–4 gate/ l ² . From this we can calculate the gate density for a 0.35 m m gate array:

This gives the core size (logic and routing only) as

We shall need to add (0.175/0.5) ¥ 2 ¥ (15 to 20) = 10.5 to 21 mil (per side) for the pad heights (we included the effects of scaling in this calculation). With a pad pitch of 5 mil and roughly 166/4 = 42 I/Os per side (not counting any power pads), we need a die at least 5 ¥ 42 = 210 mil on a side for the I/Os. Thus the die size must be at least 210 ¥ 210 = 4.4 ¥ 10 ⁴ mil ² to fit 166 I/Os. Of this die area only 1.19 ¥ 10 ⁴ /(4.4 ¥ 10 ⁴ ) = 27 % (at most) is used by the core logic. This is a severely pad-limited design and we need to rethink the partitioning of this system.

Table 15.4 shows some typical areas for datapath elements. You would use many of these datapath elements in floating-point arithmetic (these elements are large—you should not use floating-point arithmetic unless you have to):

• A leading-one detector with barrel shifter normalizes a mantissa.
• A priority encoder corrects exponents due to mantissa normalization.
• A denormalizing barrel shifter aligns mantissas.
• A normalizing barrel shifter with a leading-one detector normalizes mantissa subtraction.

TABLE 15.3  Some useful numbers for ASIC estimates, normalized to a 1 m m technology unless noted.
Parameter	Typical value	Comment 1	Scaling
Lambda, l	0.5 m m = 0.5 (minimum feature size)	In a 1 m m technology, l ª 0.5 m m.	NA
CAD pitch	1 micron = 10 –6 m = 1 m m = minimum feature size	Not to be confused with minimum CAD grid size (which is usually less than 0.01 m m).	l
Effective gate length	0.25 to 1.0 m m	Less than drawn gate length, usually by about 10 percent.	l
I/O-pad width (pitch)	5 to 10 mil = 125 to 250 m m	For a 1 m m technology, 2LM ( l = 0.5 m m). Scales less than linearly with l .	l
I/O-pad height	15 to 20 mil = 375 to 500 m m	For a 1 m m technology, 2LM ( l = 0.5 m m). Scales approximately linearly with l .	l
Large die	1000 mil/side, 10 6 mil 2	Approximately constant	1
Small die	100 mil/side, 10 4 mil 2	Approximately constant	1
Standard-cell density	1.5 ¥ 10 –3 gate/ m m 2 = 1.0 gate/mil 2	For 1 m m, 2LM, library = 4 ¥ 10 –4 gate /l 2 (independent of scaling).	1/ l 2
Standard-cell density	8 ¥ 10 –3 gate/ m m 2 = 5.0 gate/mil 2	For 0.5 m m, 3LM, library = 5 ¥ 10 –4 gate/ l 2 (independent of scaling).	1/ l 2
Gate-array utilization	60 to 80 %	For 2LM, approximately constant	1
	80 to 90 %	For 3LM, approximately constant	1
Gate-array density	(0.8 to 0.9) ¥ standard cell density	For the same process as standard cells	1
Standard-cell routing factor = (cell area + route area)/cell area	1.5 to 2.5 (2LM) 1.0 to 2.0 (3LM)	Approximately constant	1
Package cost	$0.01/pin, “penny per pin”	Varies widely, figure is for low-cost plastic package, approximately constant	1
Wafer cost	$1 k to $5 k average $2 k	Varies widely, figure is for a mature, 2LM CMOS process, approximately constant	1

TABLE 15.4  Area estimates for datapath functions. 2
Datapath function	Area per bit/ l 2	Area/ l 2 (32-bit)	Area/ l 2 (64-bit)
High-speed comparator (4–32 bit)	24,000	7.7E + 05	1.5E + 06
High-speed comparator (32–128 bit)	28,800	9.2E + 05	1.8E + 06
Leading-one detector ( n -bit)	7200 log 2 n	1.2E + 06	2.8E + 06
All-ones detector ( n -bit)	6000 + 800 log 2 n	3.2E + 05	6.9E + 05
Priority encoder ( n -bit)	19,000 + 1400 log 2 ( n – 2)	8.4E + 05	1.8E + 06
Zero detector ( n -bit)	5500 + 800 log 2 n	3.0E + 05	6.6E + 05
Barrel shifter/rotator ( n- by m -bit)	19,000 + 1000 n + 1600 m	3.4E + 06	1.2E + 07
Carry-save adder	24,000	7.7E + 05	1.5E + 06
Digital delay line ( n delay stages, t output taps)	12,000 + 6000 n + 8400 t	1.5E + 07	6.0E + 07
Synchronous FIFO ( n -bit)	34,000 + 9600 n	1.1E + 07	4.1E + 07
Multiplier-accumulator ( n -bit)	190,000 + 18,000 n	2.4E + 07	8.5E + 07
Unsigned multiplier ( n- by m -bit)	54,000 + 18,000 ( n – 2)	1.9E + 07	7.4E + 07
2:1 MUX	7200	2.3E + 05	4.6E + 05
8:1 MUX	29,000	9.2E + 05	1.8E + 06
Low-speed adder	28,000	8.8E + 05	1.8E + 06
2901 ALU	41,000	1.3E + 06	2.6E + 06
Low-speed adder/subtracter	30,000	9.6E + 05	1.9E + 06
Sync. up–down counter with sync. load and clear	43,000	1.4E + 06	2.8E + 06
Low-speed decrementer	14,000	4.6E + 05	9.2E + 05
Low-speed incrementer	14,000	4.6E + 05	9.2E + 05
Low-speed incrementer/decrementer	20,000	6.5E + 05	1.3E + 06

Most datapath elements have an area per bit that depends on the number of bits in the datapath (the datapath width). Sometimes this dependency is linear (for the multipliers and the barrel shifter, for example); in other elements it depends on the logarithm (to base 2) of the datapath width (the leading one, all ones, and zero detectors, for example). In some elements you might expect there to be a dependency on datapath width, but it is small (the comparators are an example).

The area estimates given in Table 15.4 can be misleading. The exact size of an adder, for example, depends on the architecture: carry-save, carry-select, carry-lookahead, or ripple-carry (which depends on the speed you require). These area figures also exclude the routing between datapath elements, which is difficult to predict—it will depend on the number and size of the datapath elements, their type, and how much logic is random and how much is datapath.

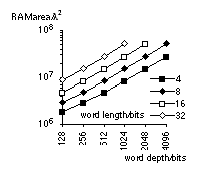
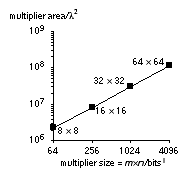
Figure 15.3 (a) shows the typical size of SRAM constructed on an ASIC. These figures are based on the use of a RAM compiler (as opposed to building memory from flip-flops or latches) using a standard CMOS ASIC process, typically using a six-transistor cell. The actual size of a memory will depend on (1) the required access time, (2) the use of synchronous or asynchronous read or write, (3) the number and type of ports (read–write), (4) the use of special design rules, (5) the number of interconnect layers available, (6) the RAM architecture (number of devices in RAM cell), and (7) the process technology (active pull-up devices or pull-up resistors).

(a)	(b)
FIGURE 15.3  (a) ASIC memory size. These figures are for static RAM constructed using compilers in a 2LM ASIC process, but with no special memory design rules. The actual area of a RAM will depend on the speed and number of read–write ports. (b) Multiplier size for a 2LM process. The actual area will depend on the multiplier architecture and speed.

The maximum size of SRAM in Figure 15.3 (a) is 32 k-bit, which occupies approximately 6.0 ¥ 10 ⁷ l ² . In a 0.5 m m process (with l = 0.25 m m), the area of a 32 k-bit SRAM is 6.0 ¥ 10 ⁷ ¥ 0.25 ¥ 0.25 = 3.75 ¥ 10 ⁶ m m ² (or about 2 mm on a side—a large piece of silicon). If you need an SRAM that is larger than this, you probably need to consult with your ASIC vendor to determine the best way to implement a large on-chip memory. Figure 15.3 (b) shows the typical sizes for multipliers. Again the actual multiplier size will depend on the architecture (Booth encoding, Wallace tree, and so on), the process technology, and design rules. Table 15.5 shows some estimated gate counts for medium-size functions corresponding to some popular ASSP devices.

[ Chapter start ] [ Previous page ] [ Next page ]